Advent Of Corona - Day 6

Solving a binary reversing challenge with Ghidra

March 27, 2020

This post is about the day 6 problem of the Advent Of Corona challenge.

The problem

You are given a binary named lagrange_baby. That’s all.

The solution

The first thing to do when you get a binary in a CTF-like challenge like this is taking a look at what bash commands like file or strings output you.

$ file lagrange_baby
lagrange_baby: ELF 64-bit LSB shared object, x86-64, version 1 (SYSV),
dynamically linked, interpreter /lib64/l,
for GNU/Linux 3.2.0, BuildID[sha1]=76154f43151d7962511001b781c47a617a01b9bd,
not stripped

$ strings -d lagrange_baby
/lib64/ld-linux-x86-64.so.2
libc.so.6
srand
__isoc99_scanf
puts
__stack_chk_fail
printf
strlen
malloc
__cxa_finalize
__libc_start_main
free
GLIBC_2.7
GLIBC_2.4
GLIBC_2.2.5
_ITM_deregisterTMCloneTable
__gmon_start__
_ITM_registerTMCloneTable
gfff
gfff
VUUU
VUUU
AWAVI
AUATL
[]A\A]A^A_
noup
still noup
 aaaaaaaaand stil noup
flag{\%s}
;*3$"

From these outputs we know the following things:

The binary is Linux x64 executable.
There are some interesting strings: noup, still noup, aaaaaaaaand stil noup and flag{\%s}. There is nothing similar to a flag inside it, so I can suppose that it’s generated in execution time.

Let’s take a deeper look into the binary. I choose Ghidra, but it can be done in any other GUI or terminal tool (r2, cutter, ida, …).

Playing around

Before doing anything we will try to mess around with the binary:

$ ./lagrange_baby
a
noup
$ ./lagrange_baby
1
noup
$ ./lagrange_baby
aaaaaaaaaaaaaaaaaaa
noup

Hm, interesting…

Reversing with Ghidra

The basic steps to begin analyzing a binary are the following:

Import the binary

Pretty straight-forward.

Ghidra import dialog — Importing a binary file into Ghidra

Analyze it

Just analyze all.

Ghidra analyze dialog — Running the automatic analysis in Ghidra

Reversing

First of all, I look that the functions panel and search for the main function. When you click at it it shows up a C-like decompiled view of the function.

Main function in Ghidra — Viewing the decompiled main function

One of the things I like about Ghidra is that it lets you redefine variable types and names. So you can change those definitions during the reversing and the flow is much easier to follow.

The first thing I do is redefine the main function to be int main (void) and the __isoc99_scanf to scanf. I notice that there are two scanf in the main function: 00100c17 and 00100d2e. So I redefine the values written to as input_1 and input_2.

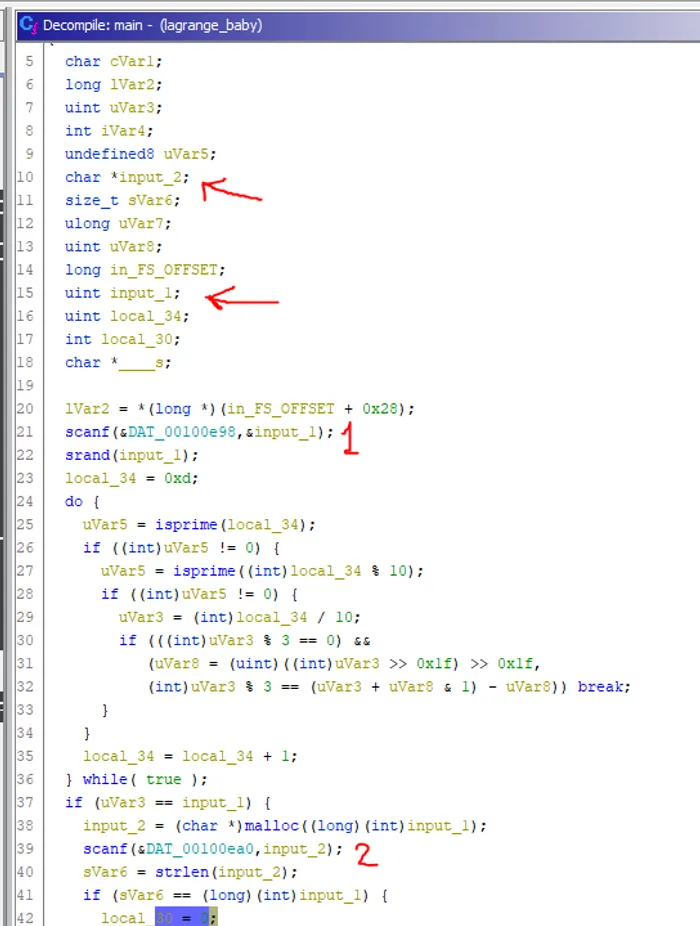
Ghidra variable redefinition — Redefining variables to improve code readability

We now know the expected types of inputs: uint input_2 and char *input_2.

As we know that the first input is a positive integer, we return and play around a bit:

$ ./lagrange_baby
0
noup
$ ./lagrange_baby
1
noup
$ ./lagrange_baby
2
noup
$ ./lagrange_baby
3
noup
$ ./lagrange_baby
4
noup
$ ./lagrange_baby
5
noup
$ ./lagrange_baby
6
a
still noup

Hm, so 6 is an accepted first input. Good, but why? We will suppose that the function isprime returns what its name says if the number given as input is prime. So if we look at the first part of the main function (I renamed some variables to make it more readable) we have the following flow

scanf(&io_input,&input_1);
srand(input_1); // init rand with seed the input value
var_1 = 0xd;    // 0xd = 13 in decimal
do {
    // this while loops var_1 from 13 untill it breaks
    var_1_prime = isprime(var_1); // Check if the current var_1 is prime
    if ((int)var_1_prime != 0) {
        // if its prime we take its remainder mod 10 and check if its prime
        var_1_prime = isprime((int)var_1 % 10);
        if ((int)var_1_prime != 0) {
            // if it is we take the integer division of var_1 by 10 and
            // check if is divisble by 3
            var_2 = (int)var_1 / 10;
            // then this strange wtf variable comes up...
            if (((int)var_2 % 3 == 0) &&
                (wtf = (uint)((int)var_2 >> 0x1f) >> 0x1f, (int)var_2 % 3 == (var_2 + wtf & 1) - wtf))
                break; // if this strange condition is satisfied we exit the loop
        }
    }
    // var_1++
    var_1 = var_1 + 1;
} while( true );

As I do not really understand this loop, I decided to implement a analogy of this in Python:

def isprime(a):
  return not (a < 2 or any(a % x == 0 for x in range(2, int(a ** 0.5) + 1)))

var_1 = 0xd

while True:
  var_1_prime = isprime(var_1)

  if var_1_prime:
    var_1_prime = isprime(var_1 % 10)

    if var_1_prime:
      var_2 = var_1 // 10
      wtf = (var_2 >> 0x1f) >> 0x1f

      if ((var_2 % 3 == 0) and (var_2 % 3 == (var_2 + wtf & 1) - wtf)):
        break

  var_1 = var_1 + 1

print(var_1, var_2)

When I run it I get this output

$ python3 loop.py
67 6

Nice! We know that var_1=67, and var_2=6. That’s where the initial 6 we found came from.

Let’s take a look at the next condition

// checks if input_1 is 6
if (var_2 == input_1) {
    // input_2 will be 6 *char
    input_2 = (char *)malloc((long)(int)input_1);
    // read input_2
    scanf(&DAT_00100ea0,input_2);
    input_2_len = strlen(input_2);
    // check if the input_2 is really 6 chars long
    if (input_2_len == (long)(int)input_1) {
        // init a var_3 to 0, which we will loop while
        // its less than 6, i.e. var_3 = 0, 1, 2, 3, 4, 5
        var_3 = 0;
        while (var_3 < (int)input_1) {
            // pick var_3-th character of the input_2
            char_i = input_2[(long)var_3];
            // evaluate some random function
            epic_function_output = epic_function(var_3 + 1);
            // check if the current character of the input (in decimal form)
            // is the same as the function return value
            if ((int)char_i != (int)epic_function_output) {
                puts("aaaaaaaaand stil noup");
                free(input_2);
                return_var = 1;
                goto LAB_00100def;
            }
            var_3 = var_3 + 1;
        }
        printf("flag{\%s}\n",input_2);
        free(input_2);
        return_var = 0;
    }
    else {
        // the message we got before
        puts("still noup");
        free(input_2);
        return_var = 1;
    }
}

Hm, interesting. Let’s try something…

$ ./lagrange_baby
6
123456
aaaaaaaaand stil noup
$ ./lagrange_baby
6
12345
still noup
$ ./lagrange_baby
6
1234567
still noup

Good. The expected input_2 length is really 6 characters long. Let’s take a look at the epic_function then. Doing some basic redefines to be more readable we have this

ulong epic_function(int x)
{
  ulong v1;
  ulong v2;
  ulong v3;
  ulong v4;

  // 0x3b9aca01 = 1000000001 in decimal
  // but what does pow_mod do?
  v1 = pow_mod(x,5,0x3b9aca01);
  v2 = pow_mod(x,4,0x3b9aca01);
  v3 = pow_mod(x,3,0x3b9aca01);
  v4 = pow_mod(x,2,0x3b9aca01);
  return v4 & 0xffffffff00000000 |
         (ulong)(uint)(int)(((double)x * -7657.00000000) / 6.00000000 +
                            ((double)(int)v4 * 10123.00000000) / 12.00000000 +
                            ((double)(int)v3 * -5861.00000000) / 24.00000000 +
                            ((double)(int)v2 * 389.00000000) / 12.00000000 +
                            ((double)(int)v1 * -13.00000000) / 8.00000000 + 0.00000000 +
                            713.00000000 + 0.50000000);
}

This function seems to do some strange calculations… Let’s take a look at pow_mod

ulong pow_mod(int x, uint y, int z)
{
  uint v1;
  int v2;
  uint v3;

  v3 = 1;
  v1 = y;
  v2 = x;
  while (v1 != 0) {
    if ((v1 & 1) != 0) {
      v3 = (int)(v2 * v3) % z;
    }
    v1 = (int)v1 >> 1;
    v2 = (v2 * v2) % z;
  }
  return (ulong)v3;
}

Hmm, I’m to lazy to understand this. Let’s try to run it! I created a C file with the pow_mod and epic_function definitions and a simple loop like it does on the lagrange_baby binary, from 0 to 5.

#include <stdio.h>

int pow_mod(int x, int y, int z)
{
  int v1;
  int v2;
  int v3;

  v3 = 1;
  v1 = y;
  v2 = x;
  while (v1 != 0) {
    if ((v1 & 1) != 0) {
      v3 = (int)(v2 * v3) % z;
    }
    v1 = (int)v1 >> 1;
    v2 = (v2 * v2) % z;
  }
  return (int)v3;
}

int epic_function(int x)
{
  int v1;
  int v2;
  int v3;
  int v4;

  // 0x3b9aca01 = 1000000001 in decimal
  // but what does pow_mod do?
  v1 = pow_mod(x,5,0x3b9aca01);
  v2 = pow_mod(x,4,0x3b9aca01);
  v3 = pow_mod(x,3,0x3b9aca01);
  v4 = pow_mod(x,2,0x3b9aca01);
  return v4 & 0xffffffff00000000 |
         (int)(int)(int)(((double)x * -7657.00000000) / 6.00000000 +
                            ((double)(int)v4 * 10123.00000000) / 12.00000000 +
                            ((double)(int)v3 * -5861.00000000) / 24.00000000 +
                            ((double)(int)v2 * 389.00000000) / 12.00000000 +
                            ((double)(int)v1 * -13.00000000) / 8.00000000 + 0.00000000 +
                            713.00000000 + 0.50000000);
}

int main() {
    for (int i = 0; i < 6; ++i)
    {
        printf("%d %d %c\n", i+1, epic_function((int)(i+1)), epic_function((int)(i+1)));
    }
    return 0;
}

Note that I changed all uint and ulong to int. When I compile and execute this I get the following output:

$ gcc epic.c
$ ./a.out
1 67 C
2 48 0
3 114 r
4 111 o
5 78 N
6 52 4

Oh! This look like something. We got the string: C0r0N4! Let’s try it as second input:

$ ./lagrange_baby
6
C0roN4
flag{C0roN4}

Yes! We got it. Not that hard, right?

Actual C code for the binary

If any of you are interested in how I created this challenge, here is the C code that generated it:

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>

#define TOO_BIG 1e+9+1

int pow_mod(int a, int x, int n)
{
   int r = 1;

   while (x)
   {
      if ((x & 1) == 1)
         r = a * r % n;

      x >>= 1;
      a = a * a % n;
   }

   return r;
}

int epic_function(int x)
{
   double s = 0;

   s += -13 * (double)pow_mod(x, 5, TOO_BIG) / 8;
   s += 389 * (double)pow_mod(x, 4, TOO_BIG) / 12;
   s += -5861 * (double)pow_mod(x, 3, TOO_BIG) / 24;
   s += 10123 * (double)pow_mod(x, 2, TOO_BIG) / 12;
   s += -7657 * (double)x / 6;
   s += 713;

   return (int)(s + 0.5);
}

int rand_between(int a, int b) { return a + (int)((double)(b - a + 1) * rand() / (TOO_BIG + 1.0)); }

int isprime(int n)
{
   int k = 5;

   if (n == 2 || n == 3)
      return 1;
   if (n <= 1 || !(n & 1))
      return 0;

   int s = 0;
   for (int m = n - 1; !(m & 1); ++s, m >>= 1)
      ;

   int d = (n - 1) / (1 << s);

   for (int i = 0; i < k; ++i)
   {
      int a = rand_between(2, n - 2);
      int x = pow_mod(a, d, n);

      if (x == 1 || x == n - 1)
         continue;

      for (int r = 1; r <= s - 1; ++r)
      {
         x = pow_mod(x, 2, n);
         if (x == 1)
            return 0;
         if (x == n - 1)
            goto LOOP;
      }

      return 0;
   LOOP:
      continue;
   }

   return 1;
}

int main()
{
   int y;

   scanf("\%d", &y);
   srand(y);

   for (int i = 13;; i++)
   {
      if (isprime(i) && isprime(i % 10))
      {
         int tmp = i / 10;

         if (!(tmp % 3) && (tmp % 3 == tmp % 2))
         {
            if (tmp == y)
               break;
            else
            {
               printf("noup\n");
               return 1;
            }
         }
      }
   }

   char *x = (char *)malloc(y * sizeof(char));
   scanf("\%s", x);

   if (strlen(x) != y)
   {
      printf("still noup\n");
      free(x);
      return 1;
   }

   for (int i = 0; i < y; i++)
   {
      if ((int)x[i] != epic_function(i + 1))
      {
         printf("aaaaaaaaand stil noup\n");
         free(x);
         return 1;
      }
   }

   printf("flag{\%s}\n", x);
   free(x);

   return 0;
}